学校C艹课的大作业，舍友和我准备搞个仿windows计算器的计算器（预计会加积分、计算矩阵计算什么的功能进去），我负责一部分的算法模块，这就顺手搬过来和大家分享一下，大伙无聊的时候可以来看看（

其实感觉不如向晚...有趣

这个是参考资料链接。

下面是目前效果预览图：（外观是C艹之神舍友用Qt做的，sdlwsl）

那么就开始正文吧，这篇文章主要会分享3个比较简单的内容，分别是：

表达式合法性检验；

表达式中缀转后缀；

后缀表达式计算。

一、合法性检验：

1. 多个运算符重复出现：

例如：19 ++ 19

实现方法：实时扫描表达式，在扫描到运算符时额外进入新判断分支，若下一个字符仍是运算符，则报错多个运算符重复出现。

2. 括号不匹配：

例如：19 + ( 19*8 ) ) - 10

实现方法：建立一个变量bracket用于统计左右括号的个数

当检测到一个’(’时，bracket+=1;

当检测到一个’)’时，bracket-=1;

同时实时检测bracket是否==0，如不是，则报错括号不匹配。

3. 除数为零：

该部分合法性检验涉及到运算过程中才出现的除数为零，故不进行实时合法性检验，并由编译器进行自动报错。

二、表达式中缀转后缀：

1. 为什么要中缀转后缀?

中缀表达式让人读起来比较好理解，但是计算机处理起来就很麻烦，因为运算顺序往往因表达式的内容而定，不具规律性（先乘除再加减，有括号先算括号）。所以计算机在进行表达式计算前，都需要对表达式进行预处理，即将中缀表达式转为后缀表达式。因为后缀表达式具有从左到右进行运算、无需考虑优先级等优点，整体运算呈线性结构，对于计算机计算来说较为友好。

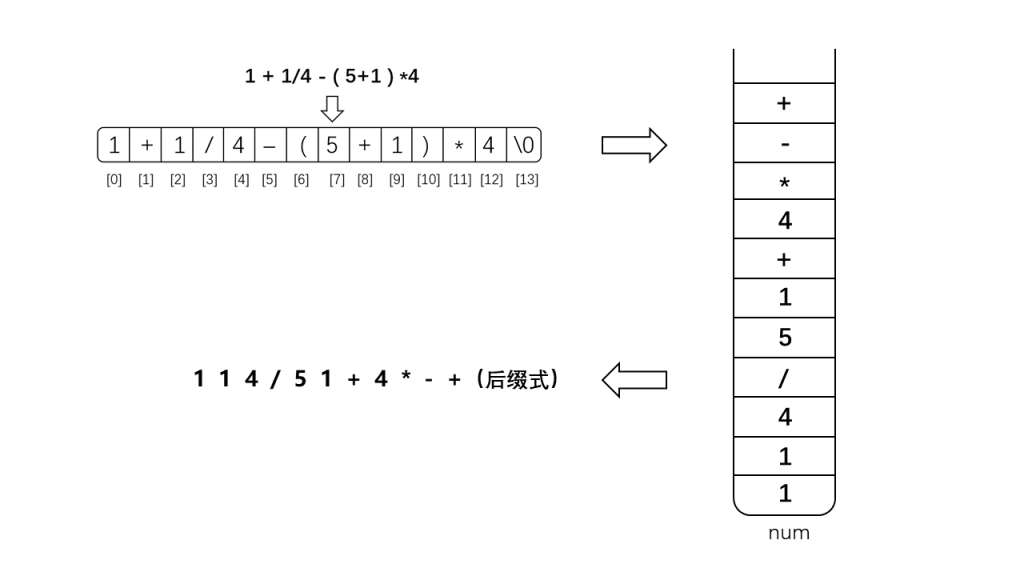
例如：1 + 1/4 - ( 5 + 1 ) * 4 (前缀)=> 1 1 4 / 5 1 + 4 * - + (后缀)

2. 中缀转后缀表达式的难点：

运算符有优先级之分：正常的表达式应该优先进行乘（*）、除（/）运算，其次在进行加（+）、减（-）的运算，中缀转后缀必须保留运算符的运算顺序。

运算符中有“(”、“)”这两个特殊符号，括号内的运算优先级最高，中缀转后缀必须保留括号内优先级最高的原则，并应该包括对括号中括号进行运算。

3.中缀转后缀表达式的实现：

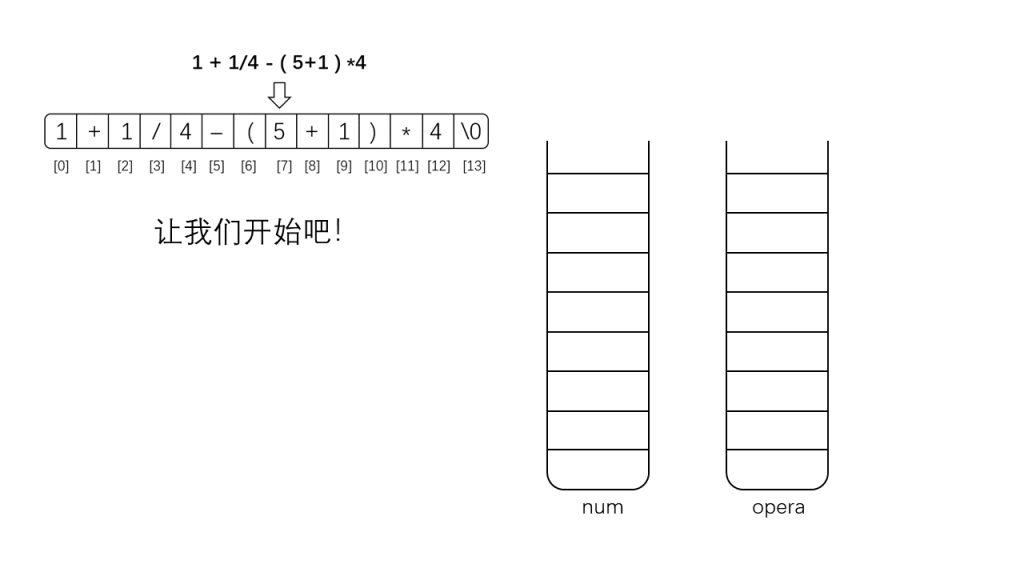
中缀转后缀实则就是对数字与运算符进行重排序，使原本的局部、分优先级的非规律计算可以通过线性计算方式实现。我们这里通过两个栈来对表达式进行重排序。

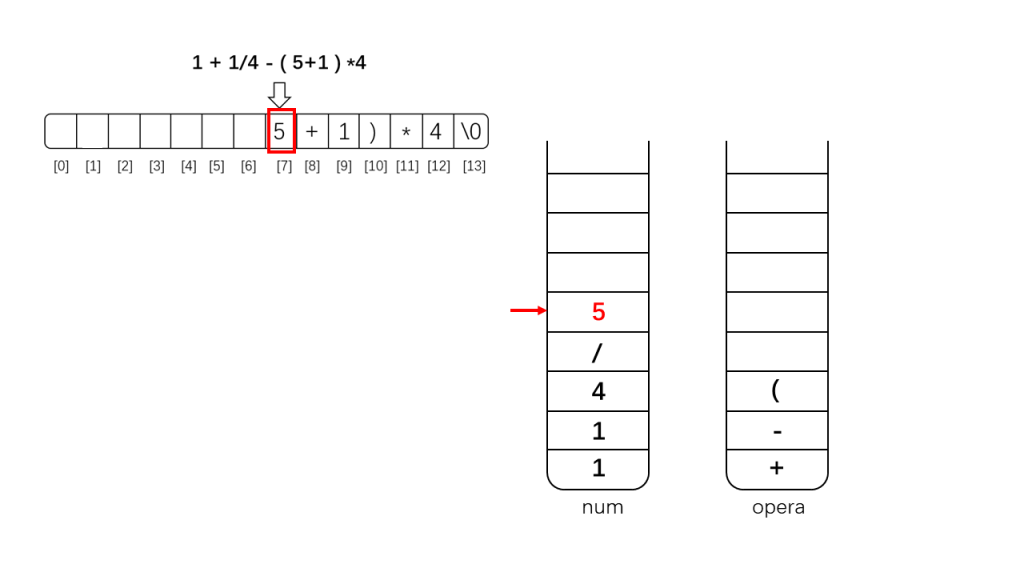
（1）从左往右扫描中缀表达式；

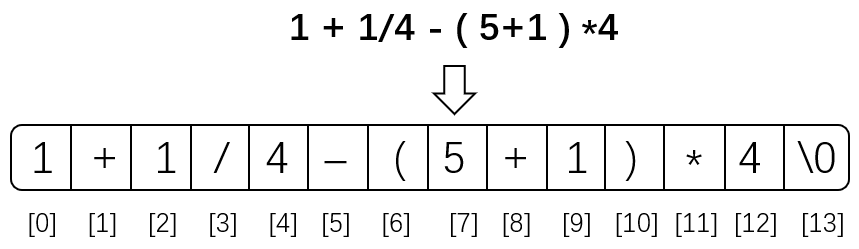
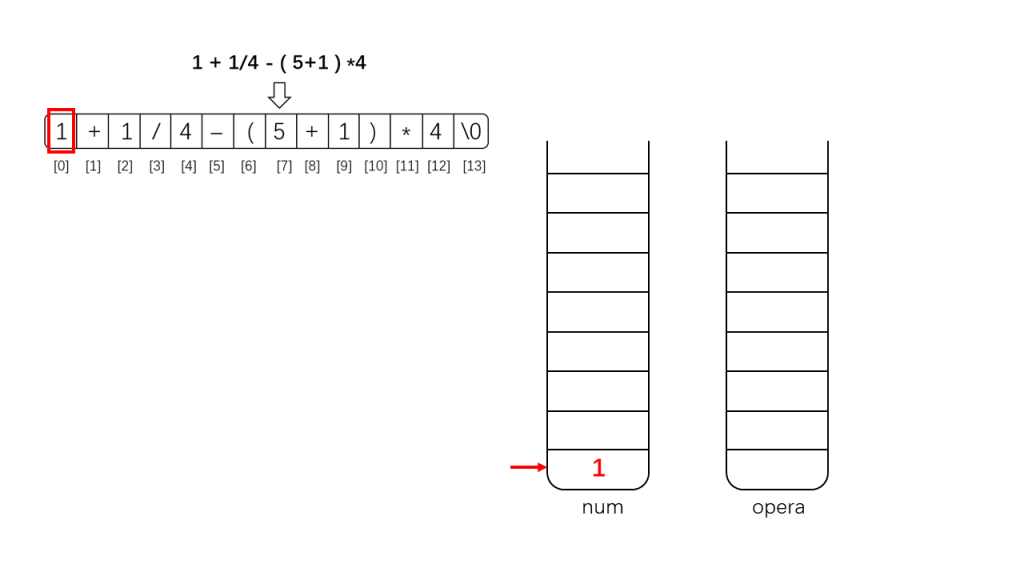
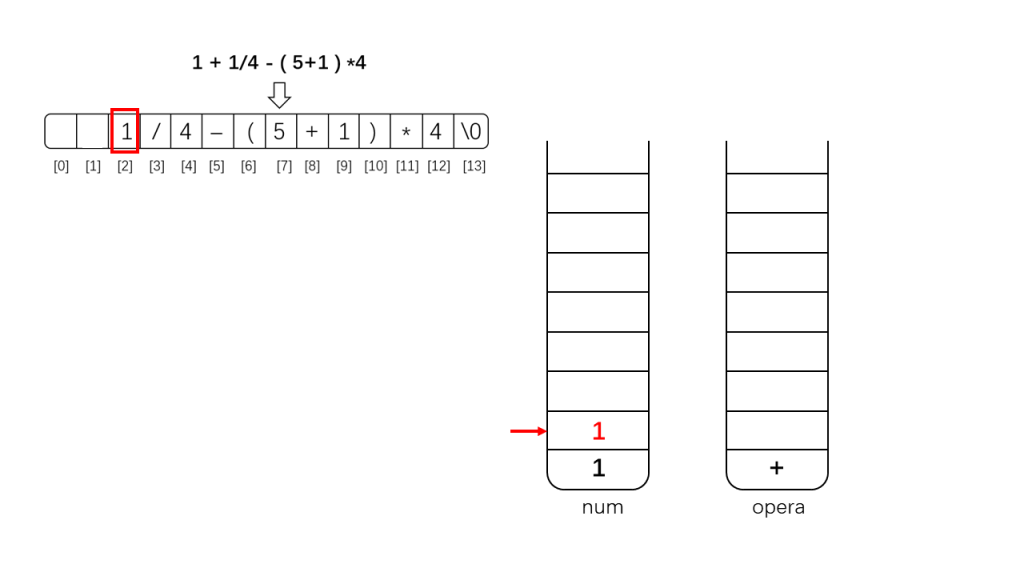
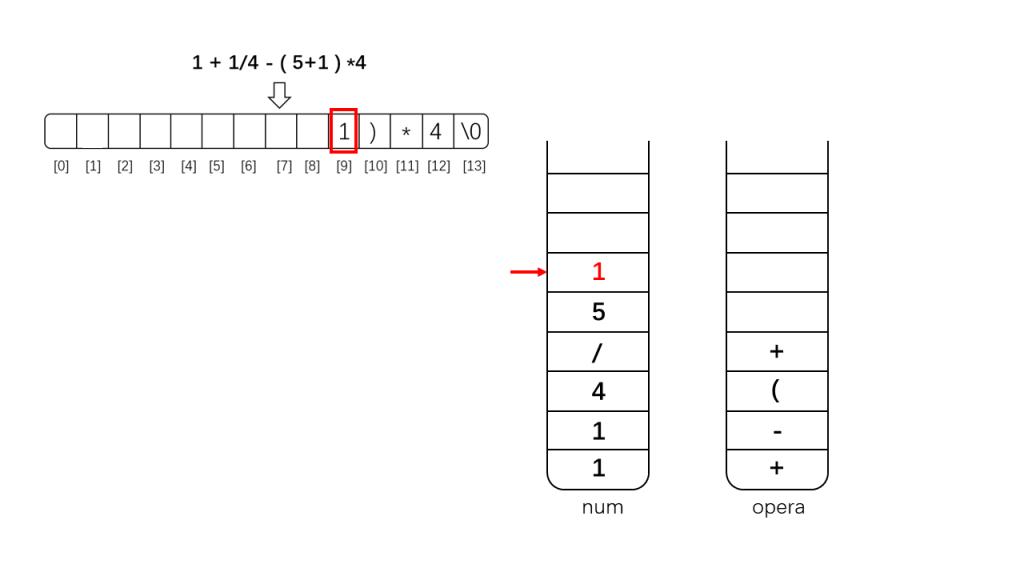
（2）如果是数字，那么将其直接入栈到栈num中；

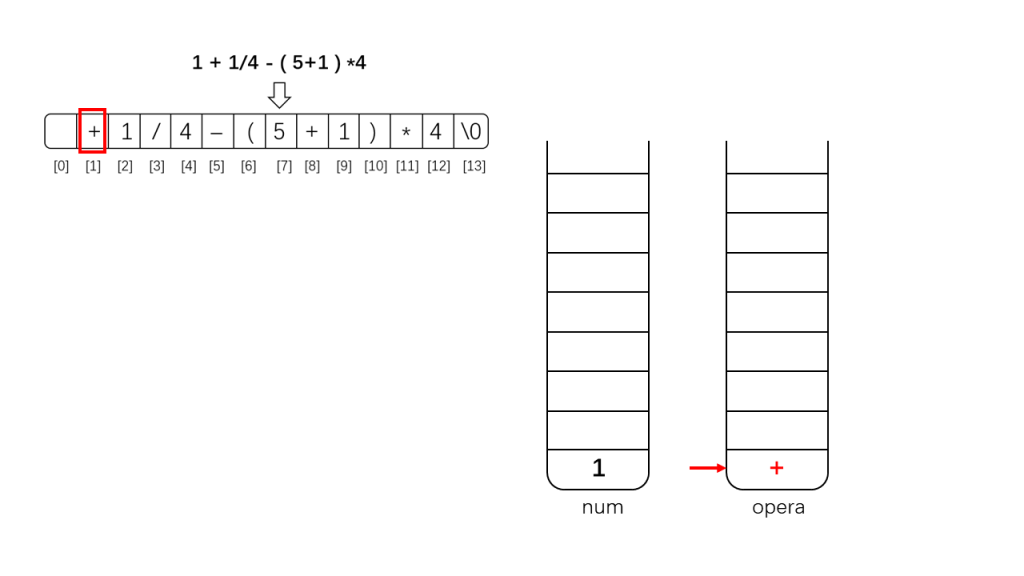
（3）如果是运算符，需要进一步判断：

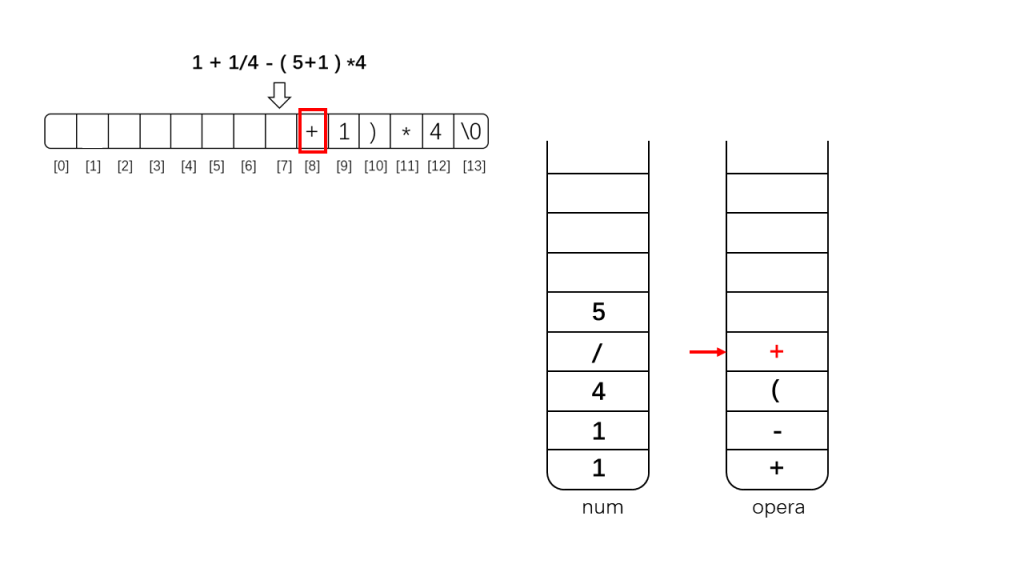
• 1 一般运算符，将该运算符与栈顶运算符进行比较：
•  如果优先级高于栈顶运算符，则直接压入堆栈opera（越靠近栈顶的运算符计算优先级越高;
• 如果优先级低于或等于栈顶运算符，则将栈opera栈顶运算符弹出并输出栈 num，然后继续比较新的栈顶运算符（弹出意味着这部分优先级提高，可以优先运算，先输出的一定是高优先级运算符；优先级相等时弹出，是因为同等优先级的条件下，弹出顺序靠前的运算符以实现从左到右运算）直到检测到优先级大于栈顶运算符或者栈opera取空，然后才将该运算符入栈opera。

• 2 左括号:
• 直接压入栈opera，（括号是最高优先级,无需比较）入栈后优先级降到最低，确保其他符号正常入栈；

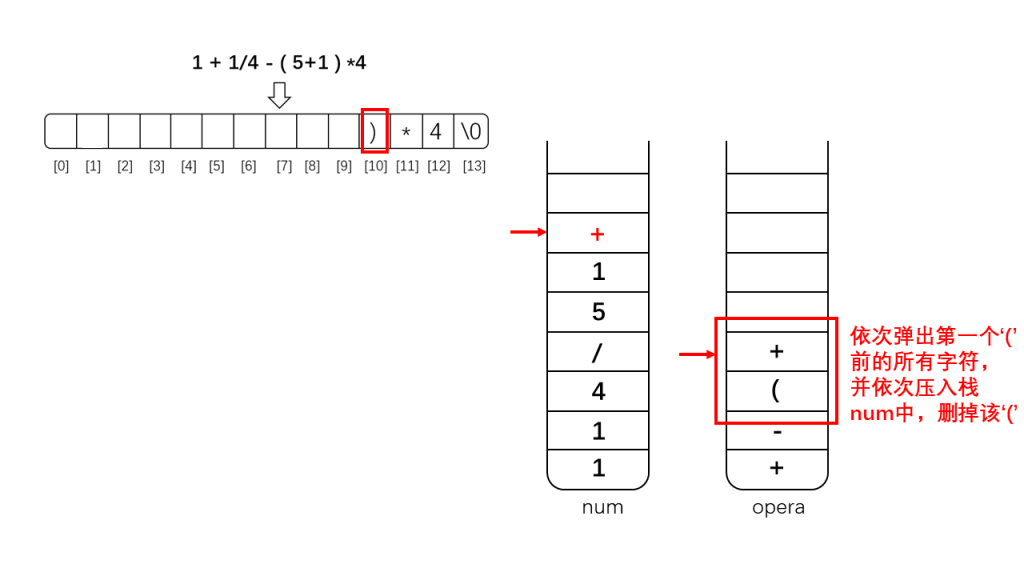
• 3 右括号:
• （意味着该括号计算过程已结束）不断弹出栈opera栈顶运算符并依次输入到栈opera，直到遇到第一个左括号。将左括号弹出栈opera但不入栈num，（即丢弃该对括号，他们作为括号，重定义运算优先级的使命已经完成）；

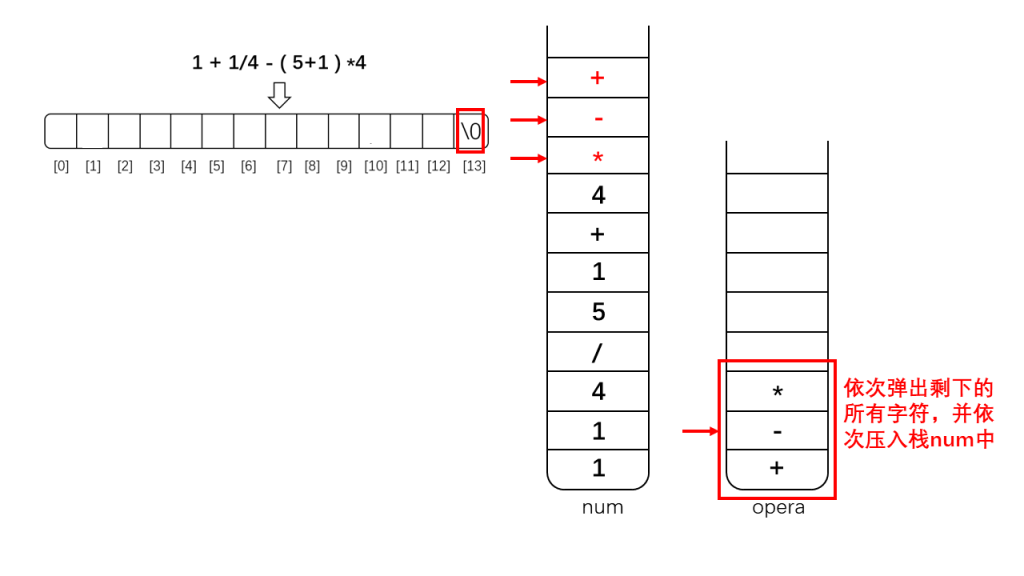
（4）如果表达式中所有字符处理完毕:

则按顺序弹出栈opera中所有剩余字符，并入栈到栈num中。此时栈num中保存的就是逆向排列（顺序需要反向）的后缀表达式。

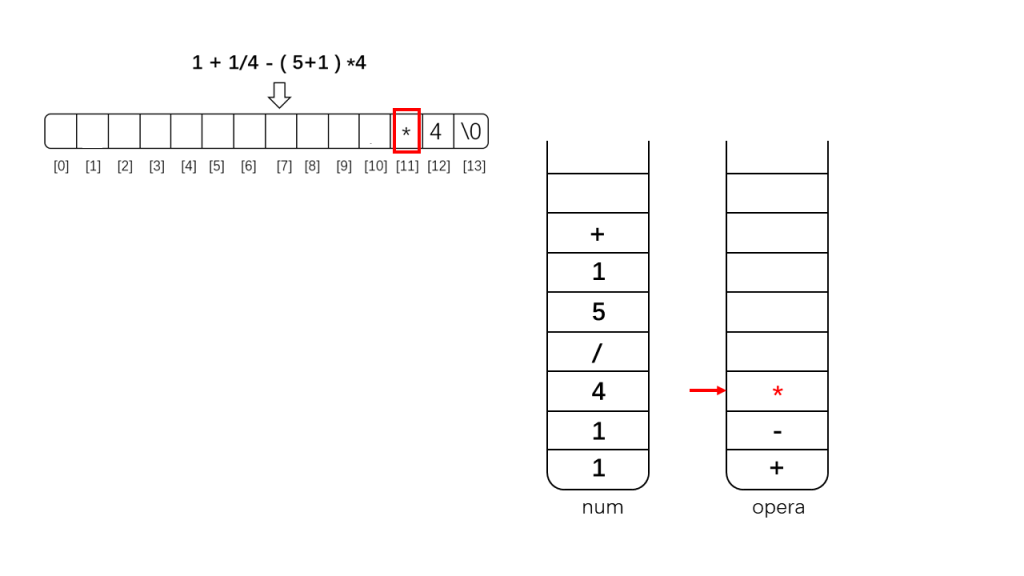
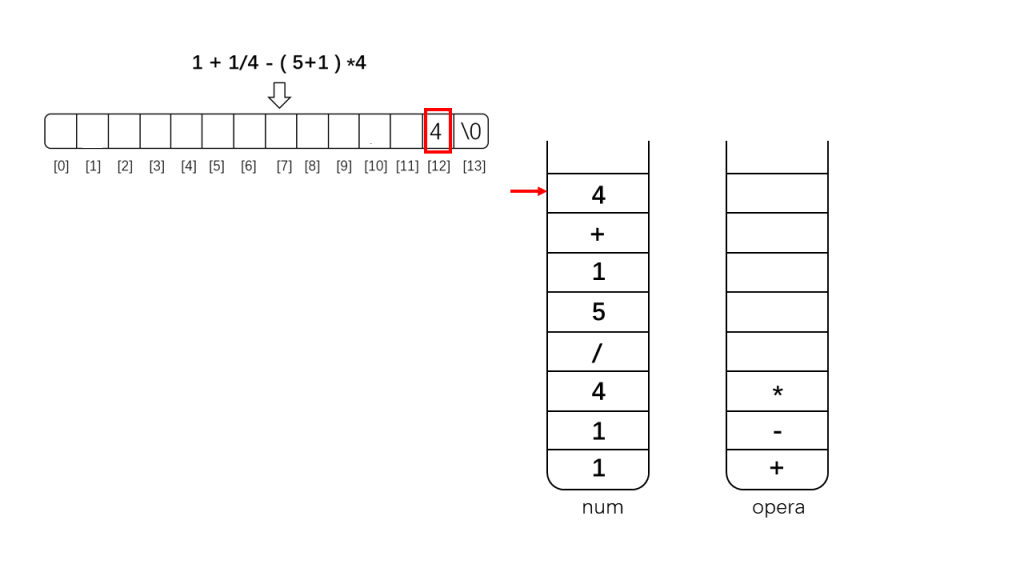
下面是示例示范：

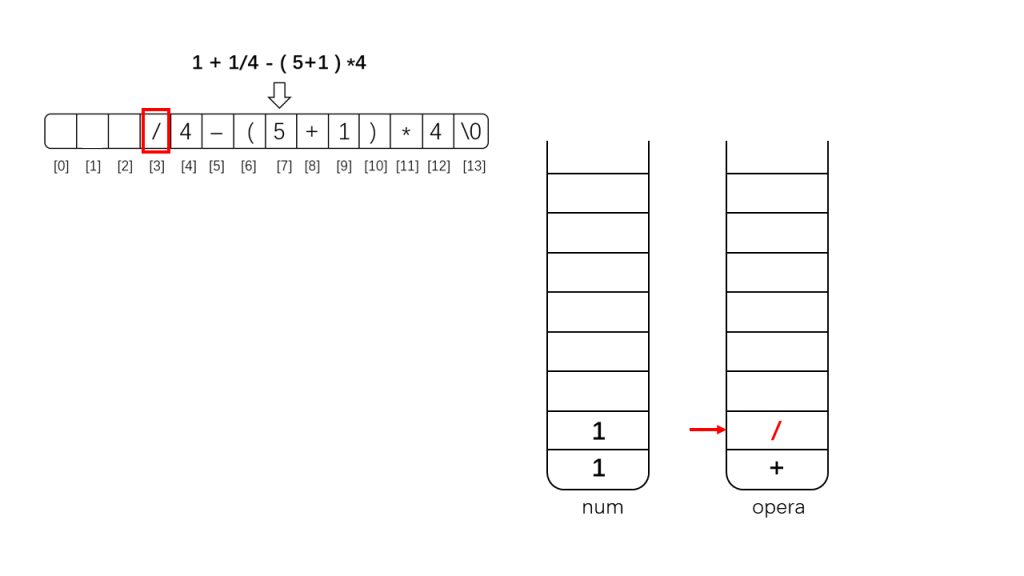
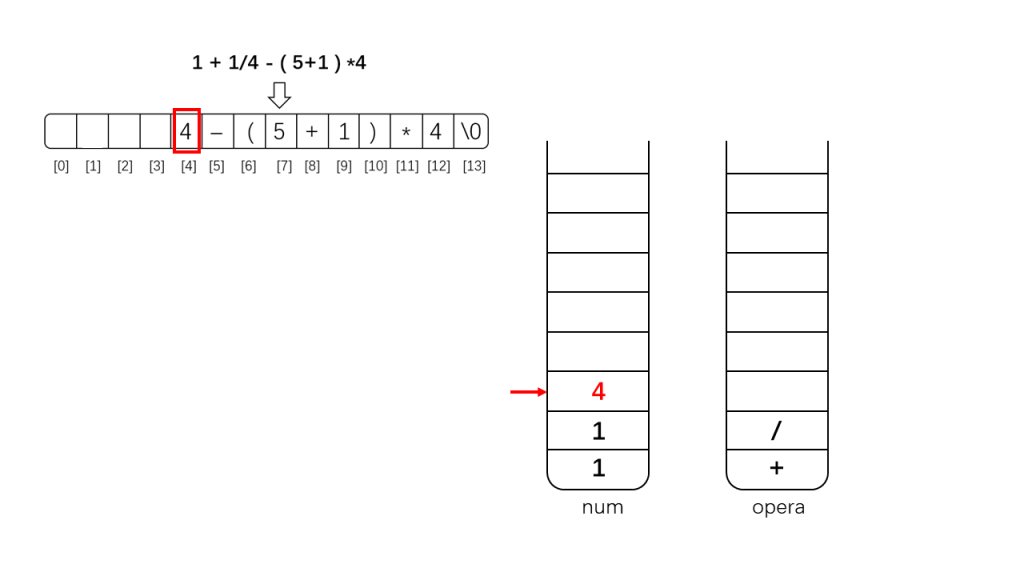
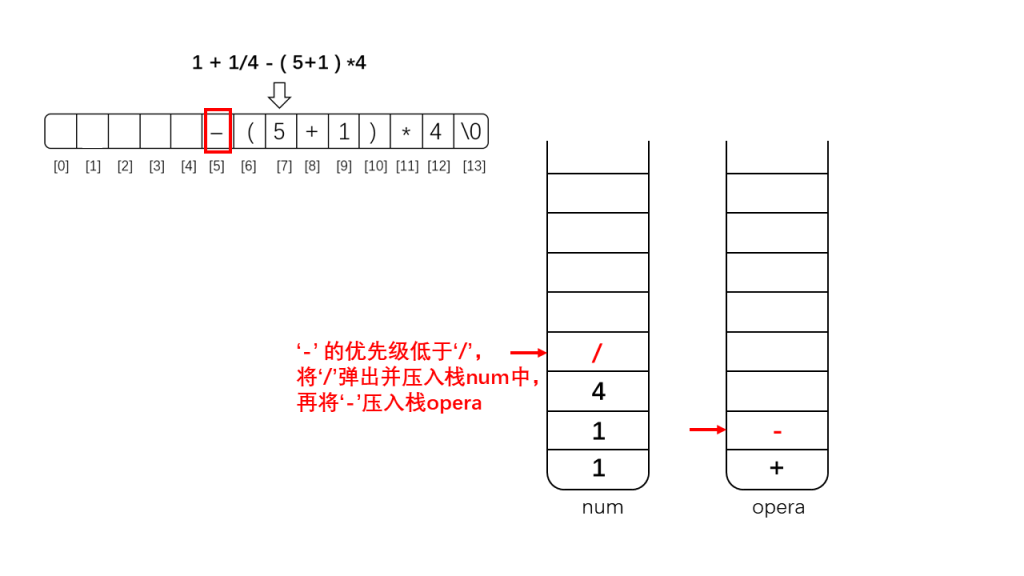
其实上面还需要把'+'也异位的，因为'-'与'+'优先级一样，为了从左向右计算应该先算'+'，这里忘记换过去了，导致这部分没有遵循从左至右原则（幸亏刚好符合加法交换律，否则这里就计算错误了）

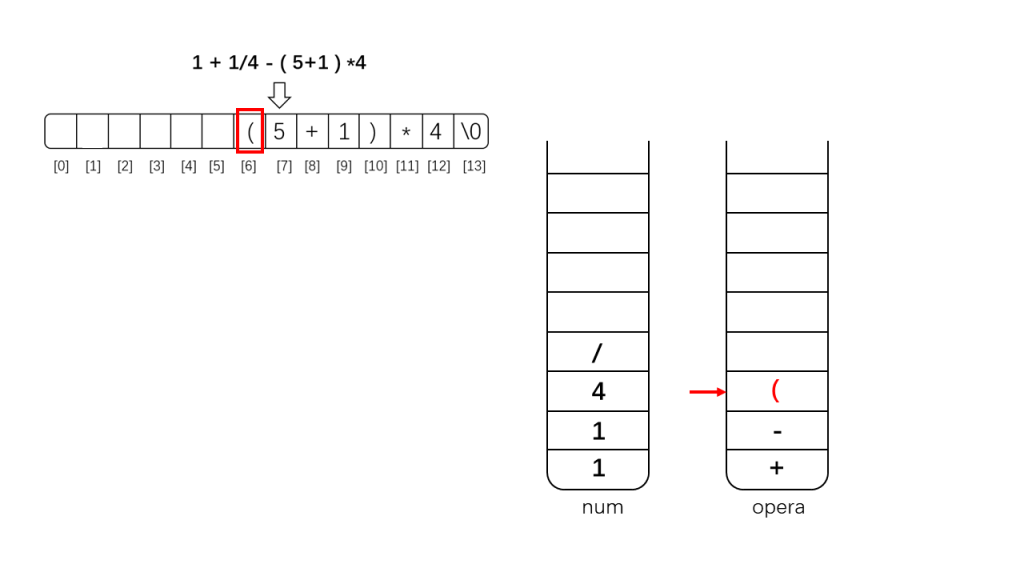
三、后缀表达式计算：

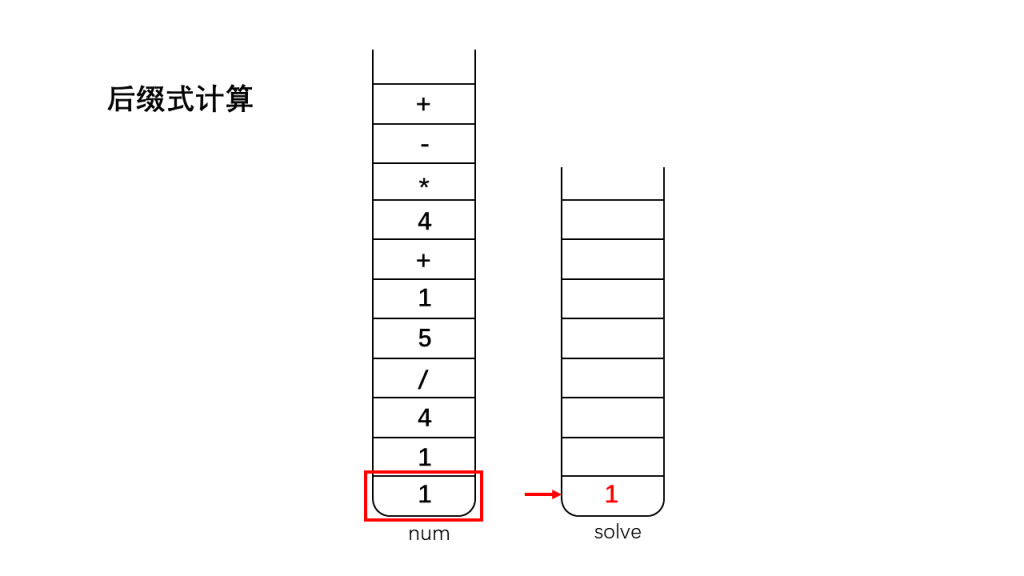
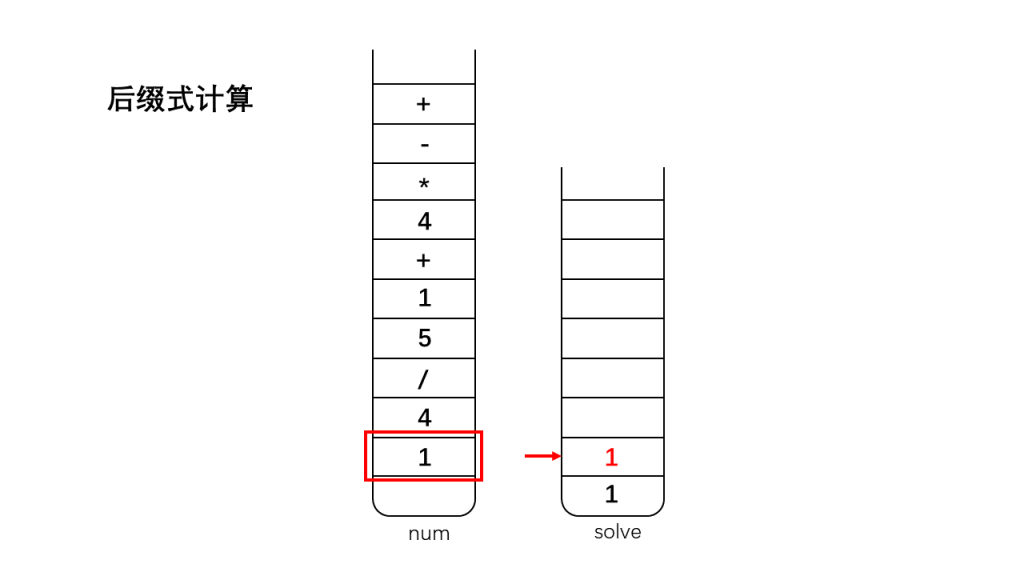
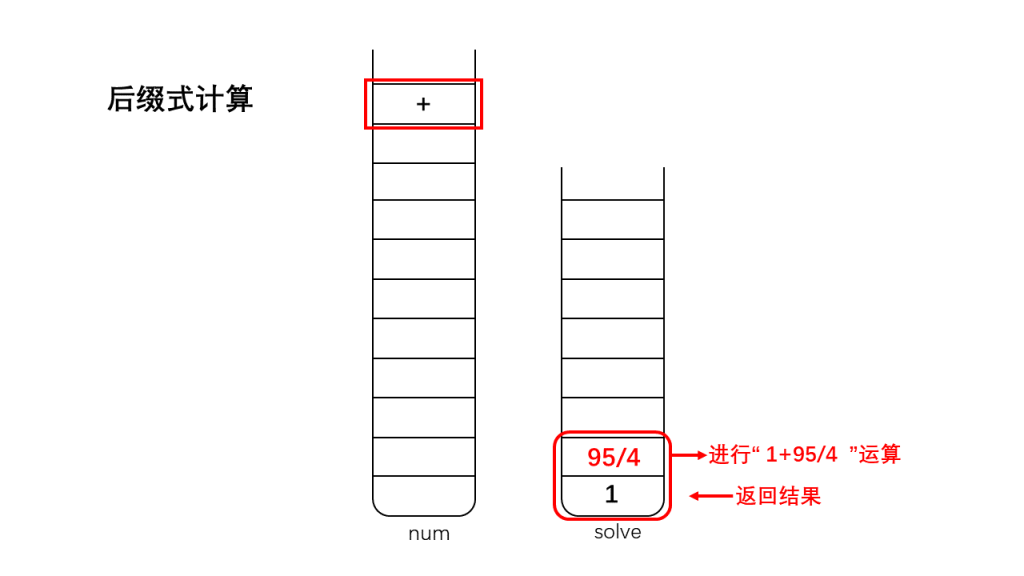
将栈num存储的字符反向弹出：

1、如果是数字，那么直接入栈到栈solve中；

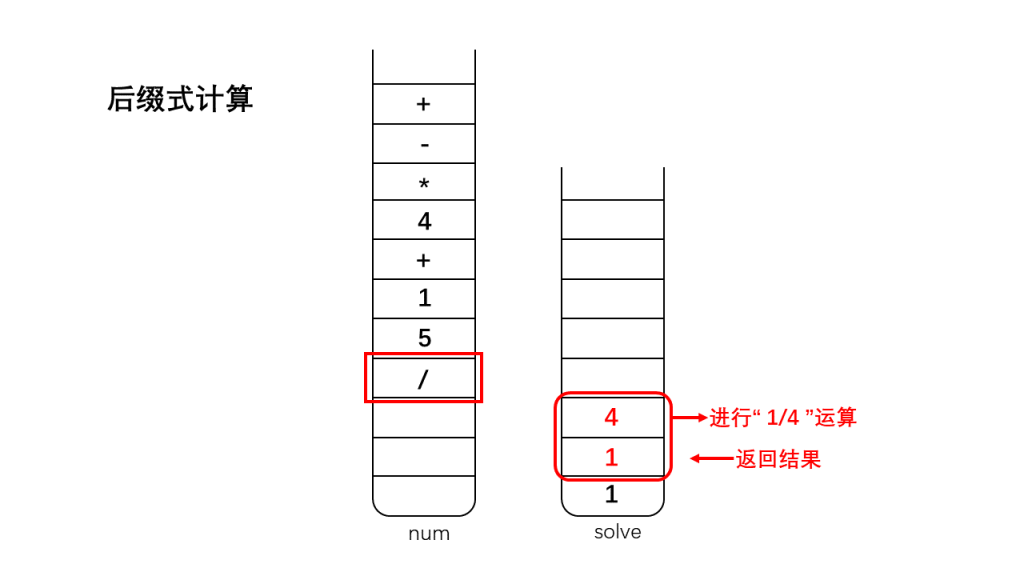
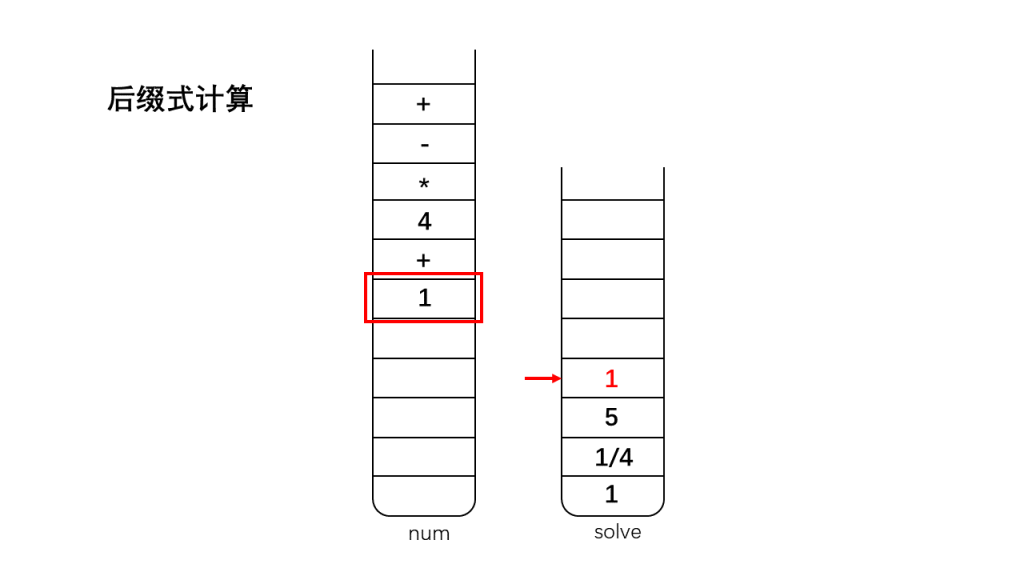
2、如果是运算符，将栈顶的两个数字出栈（因为我们考虑的运算符加、减、乘、除都是双目运算符，只需要两个操作数），出栈后对两个数字进行相应的运算，并将运算结果入栈；

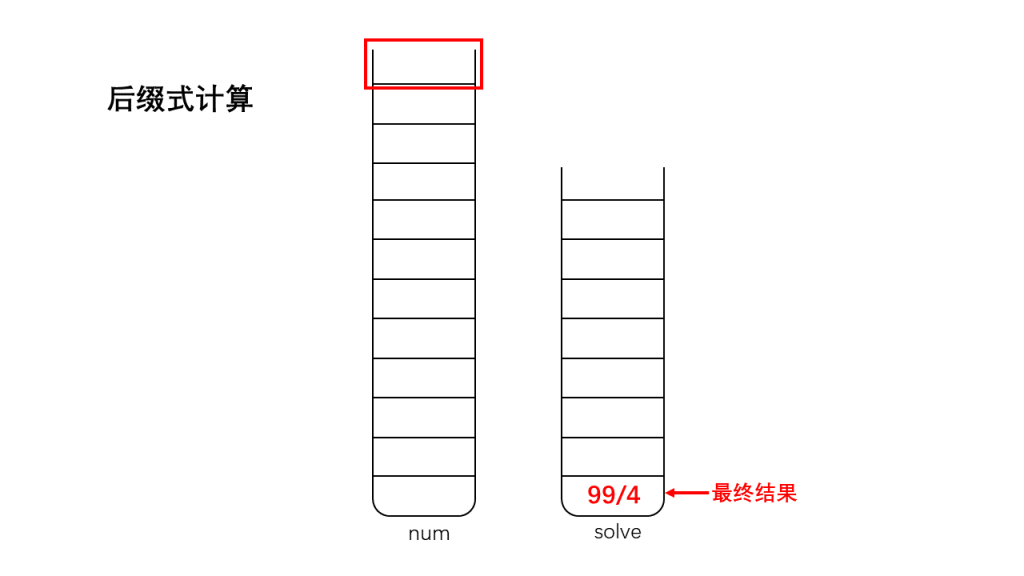
3、直到遇到'\0'，此时结束运算，此时栈solve中存储的就是表达式运算的最终结果。

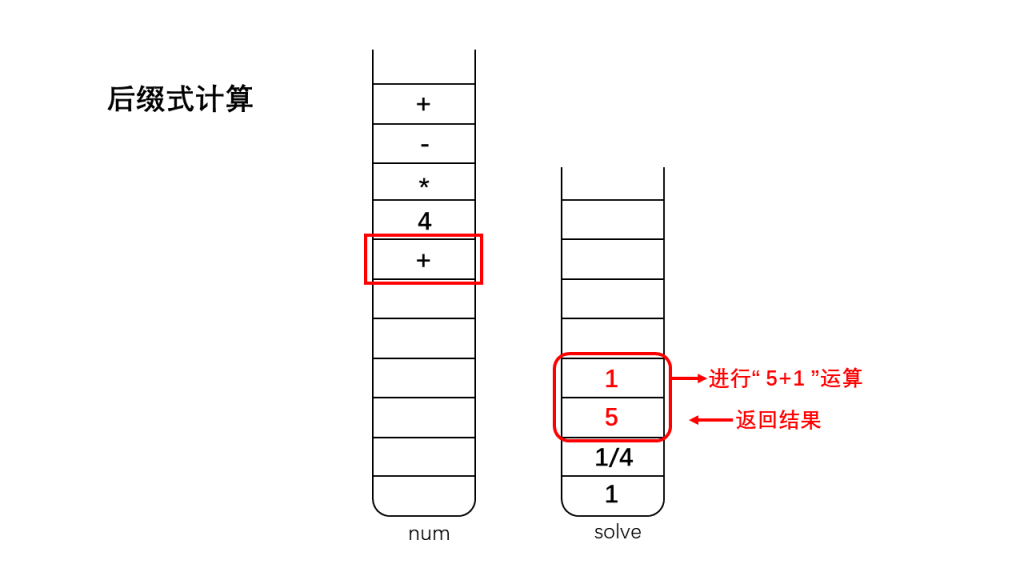
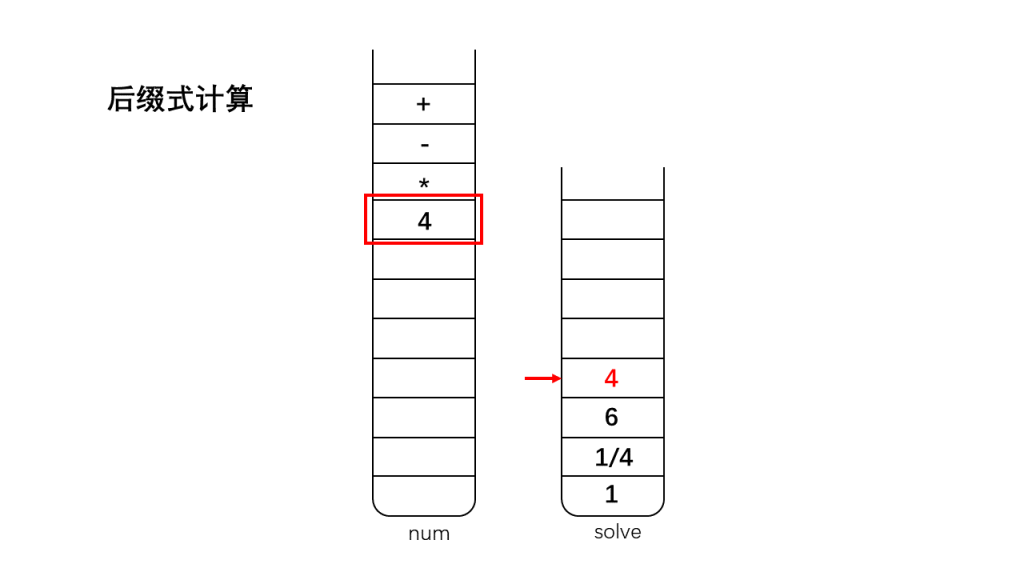
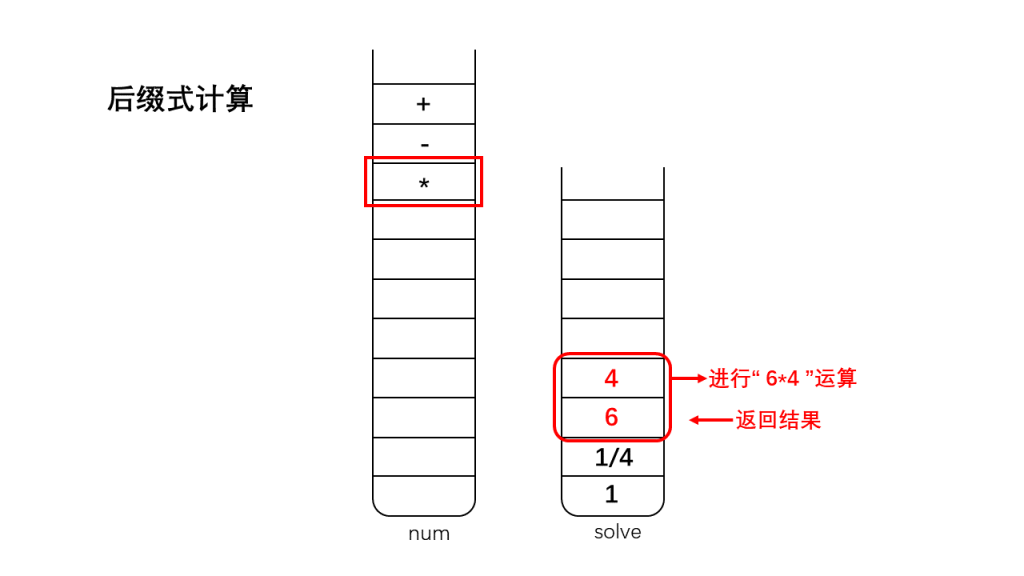
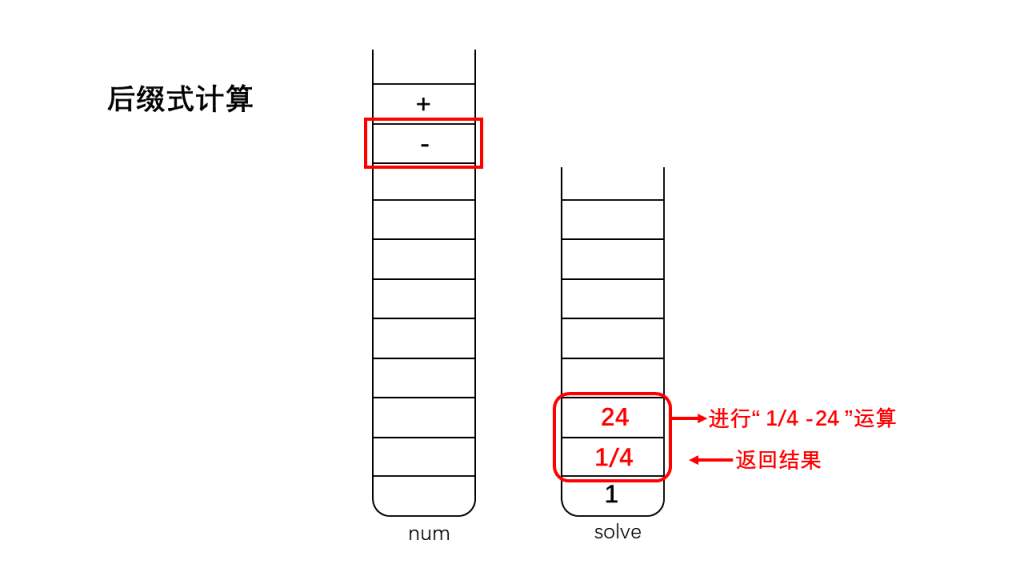
怎么样，算法很神奇吧？