通宵肝了一晚上速通,结果东西太多上考场还是忘了不少,家人们,谁懂啊
试卷难度其实不高,如果准备时间充足还是能考个八九十的,可惜了
第一章 引言
密码学基本概念
主动攻击:主动中断可用性、篡改完整性、伪造真实性
被动攻击:监听机密性 -> 获取消息内容、分析业务流
信息安全的基本属性:
- 机密性:别人看不到、看不懂
- 完整性:没被篡改伪造过
- 可用性:想看时可以被看到
- 认证:确保信息来源真实可信(消息源认证、通信实体认证)
- 不可否认性:不可抵赖信息的传输
- 可靠性:行为和结果的一致
- 可控性:被授权实体可以控制信息系统和信息使用
- 审计:活动可被追踪
密码学的概念、意义:
- 密码是指采用特定变换的方法对信息等进行加密保护、安全认证的技术、产品和服务
- 密码学是研究编制密码和破译密码的技术科学
- 密码学是保障网络空间安全的核心
- 密码学分类为:密码编码学、密码分析学
基本概念:
- 明文 M
- 密文 C
- 密钥 k
- 加密函数$C=E(k,M)$或$C=E_k(M)$
- 解密函数$M=D(k,C)$或$M=D_k(C)$
密码算法的需求:
- 可逆:知道秘密参数的使用者可以将密文恢复为明文
- 不可逆:不知道秘密参数的敌手无法恢复明文
- 秘密参数:密钥
密码算法的分类:
- 按密钥分类:
- 无密钥密码:
- 杂凑函数
- 单项置换
- 随机序列
- 对称密钥密码:
- 流密码
- 分组密码
- 消息摘要函数
- 公钥密码:
- 公钥加密
- 数字签名
- 身份认证
- 按功能分类:
- 加密算法:机密性
- 杂凑函数、消息摘要函数:完整性
- 数字签名:认证和不可否认性
密码编码学
- 中国古代
- 密钥需要保密
- 艺术成分
- 中国近代
- 豪密:密码本一次一密
- 外国古代
- 代替密码:将原有字母用其他替代,与现代密码接近
- 换位密码:不改变字母值,只交换位置,没有密钥
- 机械密码
- 明文和密文关系变得复杂
- 数学开始发挥重要作用
时间轴
- 古典密码:至1949
- 古代密码:至1800
- 凭直觉、信念设计和分析
- 多为语言学、猜谜
- 保密性基于算法的保密
- 近代密码:至1949
- 密码机
- 数学家加入
- 特点:
- 仍不是科学,是艺术
- 出现加密设备
- 出现一些算法设计基本手段:代替法、置换法
- 保密性基于算法的保密
- 里程碑:
- 1883年提出安全性应该仅仅建立在密钥的保密之上
- 现代密码:1949起
- 现代密码1:1949香农开创现代密码学:扩散和混淆原则
- 数据安全性基于密钥保密而非算法
- 现代密码2:1976公钥加密思想提出
- 公钥加密出现
- 算法更加复杂,DES成为行业标准
- 数据摘要算法出现
- 现代密码3:1994肖尔提出量子密码
- 后量子密码
密码分析学
目标:
- 恢复明文
- 恢复密钥
Kerckhoffs 假设:密码体制的安全性仅依赖于对密钥的保密,而不应依赖于算法的保密
- 假设敌手知道:
- 加密算法
- 明文概率分布
- 密钥概率分布
- 破译方法
- 加密装置
密码体制攻击方法:
- 穷举攻击
- 方法:遍历密钥
- 对抗:增加密钥数量
- 统计分析攻击
- 方法:分析密文和明文的统计规律
- 对抗:使密文和明文统计规律不一样
- 解密变换攻击
- 方法:针对加密变换的数学基础求解解密变换
- 对抗:选用具有坚实数学基础、足够复杂的算法
攻击分类(强度逐级递增)
- 惟密文攻击
- 最困难,最易抵抗
- 依赖于大计算量
- 已知明文攻击
- 从明文反推密钥
- 选择明文攻击
- 敌手发送明文得到密文,从而反推加密密钥结构
- 选择密文攻击
- 敌手发送密文得到明文,从而推测解密密钥信息
安全的分类:
- 无条件安全:不可破译
- 计算上安全:有限资源内无法破译
计算上安全的准则:
- 破译密文的代价超过被加密信息的价值
- 破译密文所花的时间超过信息的有用期
古典密码
代替密码
- 构造一个或多个密文字母表,然后用字母表中的字母或字母组代替明文的字母或字母组,各字母的相对位置不变,值改变
- 分为单表替换、多表替换
- 单表代替
- 加法密码
- $y=x+k(mod26)$,k 是密钥
- 比如凯撒密码
- 乘法密码
- $y=kx(mod26)\rightarrow x=k^{-1}y(mod26)$
- $(k,26)=1$
- 仿射密码
- $y=ax+b(mod26)$,a、b是密钥
- $x=a^{-1}(y-b)(mod26)$
- $(a,26)=1$
- 本质为加法和乘法的组合
- 分析:
- 由于相同明文加密为相同密文,故可以词频分析
- 多表代替
- 维吉尼亚密码
- 多表代换
- 将明文M分为长n个字母的多个分组$M_i$
- $C_i=AM_i+B(modN)$,A、B是密钥,A为n*n矩阵,N为字母表个数(如26)
- $M_i=A^{-1}(C_i-B)(modN)$
- 逆矩阵$A^{-1}=|A|^{-1}A^*$,其中,$|A|^{-1}$改为使用$|A|(mod\ N)$关于N的逆元,最后所得$A^{-1}$中的各个元还需再模N
第二章 流密码
基本概念
一次一密
- 优点
- 密钥只使用一次
- 无条件安全
- 加法模运算,效率高
- 缺点
- 密钥长度必须至少和明文一样长
- 密钥共享难
- 改进
- 从种子密钥生成无限长密钥(就是流密码的思想,将手动设置长密钥改为由种子生成长密钥)
流密码(序列密码)
- 逐比特加密
- ZUC、A5、SNOW、RC4
- 基本思想:利用密钥k生成密钥流,再使用密钥流加密明文
- 和分组密码区别:流密码密钥生成关乎时序逻辑,和状态有关,有记忆元件
同步流密码
- 内部状态独立于明文(否则叫自同步流密码)
- 因此同步流密码可以将密钥流生成器和加密交换器分开
好的密钥流有如下特性
- 极大的周期
- 良好的统计特性
- 抗线性分析
有限状态自动机
- 输入、输出、状态转移
密钥流生成器
- 输出符号及、状态机、状态转移函数(一般采用线性函数)、输出函数(一般采用非线性函数)
- 找出适当的状态转移函数和输出函数使密钥流满足随机性条件
- 驱动部分控制状态转移提供性能良好的序列,非线性组合子系统利用序列组合输出密钥流
二元序列的伪随机性
游程
- 如:01110为1的3游程,头尾两个0其实是圆环内的同一个0
自相关函数
- $R(t)=\sum_{k=1}^{T}(-1)^{a_k}(-1)^{a_{k+t}},0<=t<=T-1$
- $t=0$时$R=T$,其余时$R$称为异自相关函数
Golomb伪随机公设
- 一个周期内0与1个数至多差1
- 一个周期内长 $i$ 的游程占总游程数的$\frac{1}{2^i}$,且各长度的0游程与1游程个数相等
- 异自相关函数是常数(对二元序列而言异自相关函数等于-1则为伪随机序列)
- 还要满足一些条件才满足使用
- 周期足够大
- 序列要易于高速生成
- 暴露序列任意部分都无法推理后续输出(即不可预测性),此为流密码核心
线性反馈移位寄存器
反馈移位寄存器
- 组成:n个二元存储器和一个反馈函数(n级反馈移位寄存器)
- 工作:用户指定初始状态 -> 反馈函数根据序列计算候补值 -> 输出最右端 -> 整体右移,左端补上候补值
线性反馈移位寄存器LSFR
- 反馈函数$f(a_1,…,a_n)=c_1a_n\oplus…\oplus c_na_n$,c为开关,决定是否使用这级
- $a_{n_{end}+t}=a_{n_{k_1}+t}\oplus …\oplus a_t$,即$a_k$写作$a_{k+t}$
- 优点:实现简单,速度快,理论成熟
- 性质
- 输出序列完全由函数决定
- 状态数最多$2^n$
- 状态周期最多$2^n-1$
- 输出序列周期 = 状态周期
- 周期达到最大的序列即为m-序列
m-序列
特征多项式
- $a_k\rightarrow 1$,$a_{k-n}\rightarrow x^n$
产生条件
- 必要条件:特征多项式不可约(不可约不一定周期最大)
- 充要条件:特征多项式为本原多项式
- 本原多项式:不可约的n次多项式的阶为$2^n-1$
伪随机性
- 一个周期内0/1出现$2^{n-1}-1$、$2^{n-1}$次
- 一个周期内总游程数$2^{n-1}$,长为 i 的游程有$2^{n-i-1}$个,0和1游程各一半
- 异自相关函数 = -1,自相关函数 = $2^n-1$
安全性
- 已知多项式可以直接推出递推关系式
- 已知序列可以解方程(严格,用已知状态列异或方程组求各开关)或B-M算法求综合解
非线性序列
钟控序列生成器
- LSFR1输出1:LSFR2移位输出一次
- LSFR1输出0:LSFR2不移位,重复上次输出
- 周期:$\frac{T_1T_2}{gcd(w_1,T2)}$,其中w为LSFR1序列值之和(可知$T_1T_2$时必然回到初态)
第三章 分组密码
基本概念
安全性原则
- 混淆原则:将密文、明文和密钥之间的统计关系和代数关系变尽可能复杂,即使获得统计规律也无法攻击
- 扩散原则:明文中的每个位尽可能影响更多的位
- 其他要求
- 分组长度足够大
- 密钥量足够大
- 置换算法足够复杂
- 加解密简单
- 差错传播尽可能小
代换
- 明文的每个分组都产生唯一的密文分组的可逆映射
- 弱点
- 分组长度太小则可以统计分析攻击
- n比特代换结构密钥推荐大小$n2^n$比特
代换网络
SP网络
Feistel密码结构
- 分组大小:分组越大越安全,加密越慢
- 密钥大小:同上
- 轮数:多轮提供安全性,典型的轮数为16
- 子密钥产生算法:复杂性
- 轮函数:复杂性
DES
- DES是第一代公开的、完全说明细节的商业级现代加密算法
- 参数
- 明文分组长度:64位(分组不满64比特时填充数字并在最后一字节写入填充指示符PI)
- 密文分组长度:64位
- 密钥长度:64位(56位有效长度+8位奇偶校验)
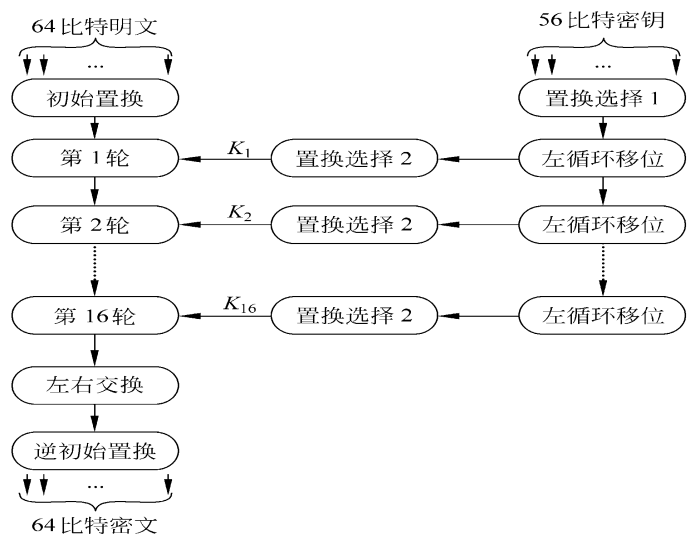
- 算法:初始置换$IP$、16轮迭代乘积变换、逆初始置换$IP^{-1}$、16个子密钥生成器
- 攻击
- 时间-空间权衡攻击
- 查分攻击
- 线性攻击(最有效)
- 相关密钥攻击
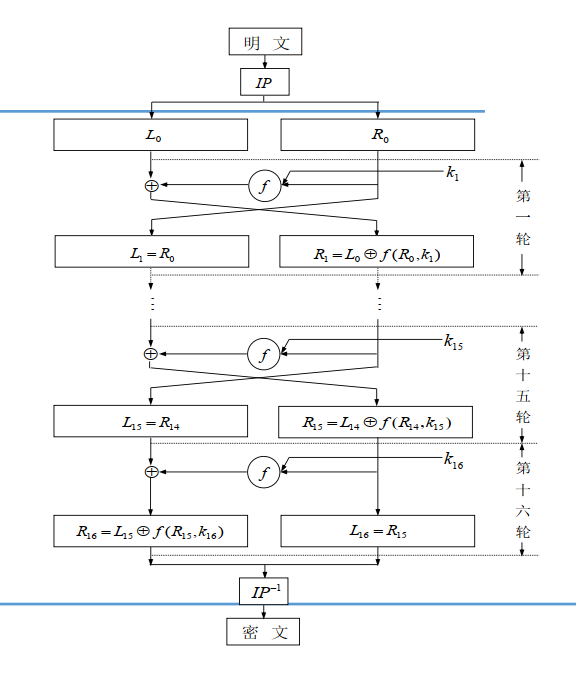
- 算法


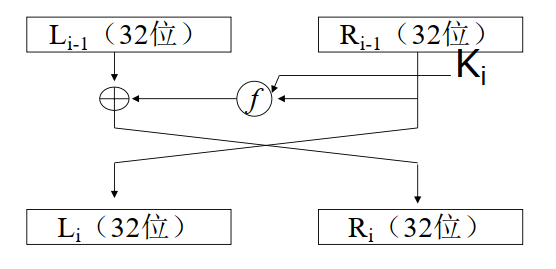
- $L_i=R_{i-1}$,$R_i=L_{i-1}\oplus F(R_{i-1},K_i)$
- 初始置换IP和逆初始置换:
- 将64位明文置换为乱序的明文
- 将64位迭代输出置换回去
- 意义仅为打乱比特间的ASCII编码关系
- 加密轮次

- 输出$F(x,y)=(y,x\oplus f_k(y))$
- 消息被划分成左右两部分,右半边作为下一轮的左半边,右半边输入轮函数后的结果与左半边异或、输出作为下一轮右半边
- 一共16轮
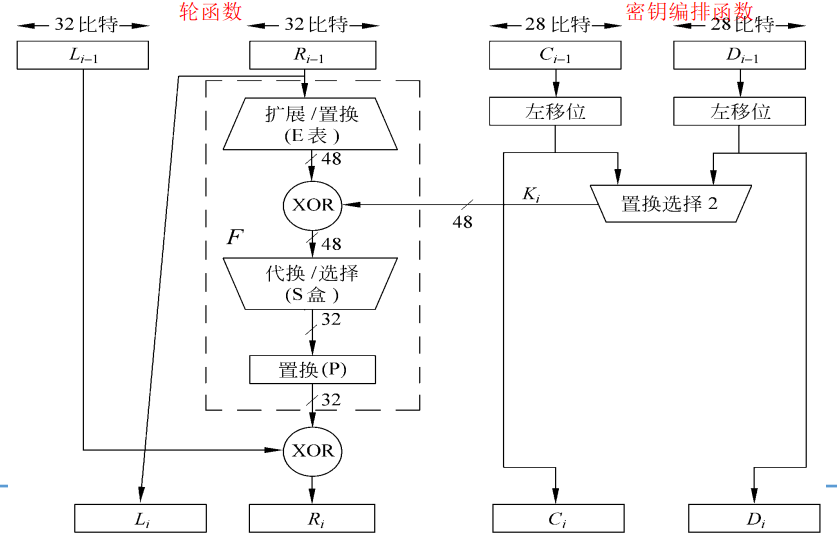
- 加密轮次内部:轮函数

- 首先通过E表置换,将32比特分组拓展到48比特然后拓展分组与密钥编排函数生成的48比特子秘钥异或然后进入S盒代换最后P盒置换输出
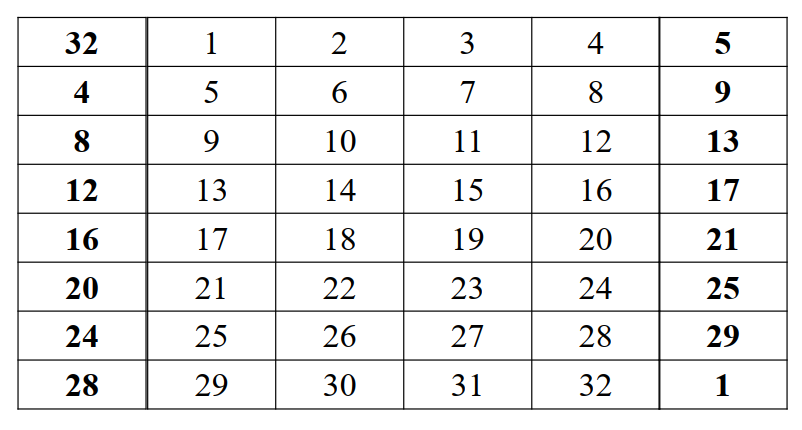
- E表

- 简单地通过补入分组的位拓展
- S盒

- DES中有8个S盒,每个S盒接受48比特消息的6比特分组,并给出4比特输出,总共32比特输出
- 运作方式如图,头末两位作行、其余位作列查询输出
- S盒作用在于混淆
- P盒
- 将S盒输出再置换一遍,输出32比特
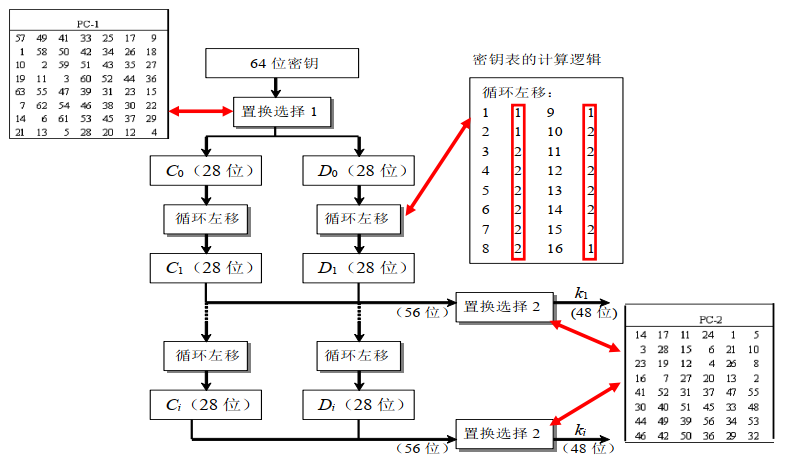
- 密钥编排

- 密钥编排作用于另一边,用于生成16轮使用的48比特子秘钥
- 首先去除64比特密钥中的8比特校验位得到56比特有效密钥
- 然后通过PC1置换一次,并划分成左右两部分
- 按轮次查询移动位数,并循环左移两部分
- 合并两部分并通过PC2置换,输出16个48比特子密钥
多重DES
- 多重DES就是使用多个密钥对明文多次加密
- 双重DES
- 利用两个不同的密钥进行两次加密
- 期望密钥长度拓展为2*56=112比特
中间相遇攻击
工作模式
- 如何选择
- ECB:加密长度小于等于分组长度
- CBC:明文不易丢信号,且没有特殊格式要求
- CFB:易丢信号环境,或对明文格式有要求
- OFB:不易丢信号,但信号易出错,明文冗余多
- 电码本ECB
- 直接利用加密算法分别对各个分组数据组加密
- 优点
- 简单
- 可并行
- 缺点
- 相同明文分组对应相同密文分组
- 统计规律和结构规律
- 应用:随机数加密、单分组明文加密
- 密码分组链接CBC
- 将明文分组与上一次密文块异或后再去加密,对于第一块明文有对应的初始向量使用
- 解密时将本轮解密出的块与上一密文块异或后才得到明文块
- 优点
- 屏蔽统计特性
- 有限的错误传播(两步)
- 自同步(丢块不影响后续密文块的解密)
- 密码反馈CFB
- 带加密消息按字符、字节或比特处理时可使用
- 反馈密文
- 特点
- 相同明文不同密文(依赖于IV)
- 链接依赖性:重排密文会影响解密
- 错误传播
- 自同步,但需要更多密文组
- 输出反馈OFB
- 反馈DES输出
- 特点
- 相同明文不同密文(依赖于IV)
- 密钥流独立于明文
- 无错误传播
- 可错误恢复,但无法自同步
- 计数器
- 可并行
- 数据块随机访问
- 可证明安全
- 简单
AES
- 三层轮函数
- 线性混合层:保证多轮的高度扩散
- 非线性层:将S盒并行使用确保混淆
- 密钥加层:子秘钥异或
- 算法
- 明文分组可变:128、192、256比特
- 密钥长度可变:同上
SM4
- 分组长度、密钥长度128比特
- 32轮非线性迭代结构
第四章 公钥密码
基本概念
对称密码缺陷
- 对称加密需要保存$\frac{N(N-1)}{2}$个密钥
- 密钥共享需要安全信道
- 且建立新用户不方便
- 没有签名功能
理论基础
- 单向函数:正易反难
- 陷门:未知某个参数时正易反难,知道后简单
优势
- 秘钥分发:可以通过公开的信道传输
- 密钥管理:每个用户保管自己的私钥和别人的N-1个公钥,系统只需维护N个公钥
- 开放系统:此前未建立关系的用户也能安全通信
用途
- 加密
- 签名
- 秘钥分配
RSA
- 密钥生成
- 选择两个大素数p、q(M-R算法)
- 计算$n=pq$,$z=(p-1)(q-1)$
- 随机选择e,且e和z互质
- 选取d使$ed\ mod\ z=1$(即e模z的逆元)
- 公钥(n,e),私钥(n,d)
- 加密与解密
- $c=m^e\ mod\ n$,公钥加密
- $m=c^d\ mod\ n$,私钥解密
- 核心:$m=(m^e\ mod\ n)^d\ mod\ n$
- 模运算性质可以显著减小中间结果
- 安全性
- 基于大素数分解困难
- 不能抵御选择密文攻击
- 攻击
- 截获密文$c_1$,对应明文$m_1$,$c_1=m_1^e(mod\ n)$
- 选取明文m构造新密文$c_2$,$c_2=c_1m^e(mod\ n)$
- 让解密者解密$c_2$,得到明文$m_2$,$m_1=m_2m^{-1}(mod\ n)$
ElGamal
- 密钥生成
- 大素数p
- p简化剩余系中选取生成元g
- $\beta =g^\alpha\ mod\ p$
- p,g,β为公钥,α为私钥
- 加密
- 随机生成秘密数k
- $r=g^kmod\ p$,$s=x\beta^kmod\ p$
- $E(x,k)=(r,s)$
- 解密
- $D(r,s)=s(r^\alpha)^{-1}mod\ p=xg^{\alpha k}g^{-\alpha k}mod\ p=x$
- 特点
- 基于离散对数难解性:循环群的离散对数问题
- 概率算法
- 不能抵御选择密文攻击
- 存在密文扩张
- k必须保密且一次一密
- 与RSA的区别
- 困难问题不同
- 公开参数设置不同
椭圆曲线密码
- 可以用更短的密钥获得同样的安全性
- 困难问题为椭圆曲线上的离散对数问题
- 明文编码为椭圆曲线上的点,再对点加密
- 优点
- 安全性高
- 密钥量小
- 灵活性好
SM2
- 基于椭圆曲线的公钥密码
- 一般160比特素数域
- 与ECC比较
- 效率高
- 时间消耗换安全性
- 密文扩张更严重
- 检错措施,增加完整性可靠性
第五章 哈希函数
基本概念
定义
- 将人异常消息映射为固定长度的值
安全条件(多项式时间内,三个条件从下可以向上推得)
- 单向性:求Hash容易,反推计算上不可行
- 抗弱碰撞性:已知x,找出y使x、y的哈希值相等计算上不可行
- 抗强碰撞性:找出任意x、y的哈希值相等计算上不可行
生日攻击
- 第一类生日攻击
- k个输入造成某输出$H(y)=H(x)$的概率
- $P=1-[1-\frac{1}{n}]^k \rightarrow \frac{k}{n}$
- 第二类生日攻击
- 寻找函数H具有相同输出的两个任意输入的攻击方式
- 相同输出的概率$P(n,k)=1-\frac{n!}{(n-k)n^k}$
- 若$P=0.5$,可得$k=1.18\sqrt{n}\rightarrow \sqrt{n}$
- 通常要求消息长度至少为128比特,DSS为160比特
MD5
- 分组:512比特
- 输出:128比特
SHA-1
- 分组:将小于$2^{64}$比特长的消息分为512比特长的分组
- 输出:160比特
- 步骤
- 填充消息长度到512倍数减64(64个空位留给后面用,且无论原长是否满足都必须填充),填充内容:1000……
- 后64位表示填充前的长度模$2^{64}$(大端,数据高字节存在低地址处)
- 使用160比特长的缓冲区存储中间结果和最终结果
- 缓冲区为5个32比特的大端寄存器,且有特定的初始值
- 对每个分组用某个压缩函数(4轮*20迭代)处理并将首轮与末轮结果相加得CV
- 最后将5*32=160比特即为输出
SM3
- 输入:长$2^{64}$
- 输出:256比特
- 步骤
- 填充:与SHA1一致
- 按512比特对消息分组
- 对每个分组按16字划分进行消息拓展,最后得到132字
- 各个分组迭代压缩,缓冲区初始值为8*32=256比特(压缩函数非线性)
- 输出256比特哈希值
- 安全性
- 压缩函数非线性,提供混淆作用,安全性很高
- 置换函数线性,提供扩散作用
- 比大部分杂凑算法安全,且效率不错
SHA-3
- 新结构:海绵函数
- 上轮迭代输出反馈到下轮
- 允许输入和输出长度可变,具有灵活性
- 安全性
- 可以抵御现有的攻击
- 目前未发现弱点
- 灵活性
- 可选参数配置
- 高效性
- 尚未广泛采用
第六章 数字签名和认证协议
基本概念
私钥加密,公钥解密
- 第三方能认证签名者,签名者不能否认签名,签名不可伪造
- 签名有消息和载体两部分
- 特点
- 可信、不可伪造、不可复制、不可改变、不可抵赖
- 构成
- 密钥生成
- 签名算法
- 验证算法
- 需求
- 容易签名
- 容易识别和验证
- 伪造不可行
RSA签名
- 签名和验证
- $s=m^dmod\ n$
- $m=s^emod\ n$
- 缺点
- 可伪造对随机消息的签名
- 可伪造对$x_1x_2$的签名(RSA的可乘性)
- 签名速度慢
- 改进
- 签名前求文件的hash
ElGamal签名
- 密钥生成

- 签名与验证
- $r=g^kmod\ p$,$s=(h(m)-xr)k^{-1}mod(p-1)$,签名即为$(r,s)$
- $y^rr^s=g^{h(m)}mod\ p$
- 缺点
- 随机数k不可泄密
- 随机数k不可重用
DSS签名
- DSS只能签名不能加密
- 密钥生成

- 签名
- $r=g^kmod\ p\ mod\ q$
- $s=(h(m)+xr)k^{-1}mod\ q$
- 签名即为$(r,s)$
- 验证
- $u_1=h(m)s^{-1}mod\ q$,$u_2=rs^{-1}mod\ q$
- $g^{u_1}y^{u_2}mod\ p\ mod\ q=r$
数字签名的一般概述

特殊体制签名
- 盲签名
- 签名者不知道将要签名的消息内容
- 希望获取签名者可以使用签名者回传的签名消息对自己的消息签名
- 应用:金融相关
- 不可否认签名
- 没有签名者的合作无法验证签名
- 应用:版权领域
- 群签名
- 群众以群的名义签名,可验证签名群,不能独立分辨签名者,可借助群成员验证签名者
- 性质
- 正确性、不可伪造、匿名、不可关联、可跟踪、可开脱、抗联合攻击
- 代理签名
- 组成
- 系统建立
- 签名权力委托
- 代理签名产生
- 代理签名验证
- 强代理签名方案的性质
- 可区分、可验证、强不可伪造、强可识别、强不可否认、防止滥用
SM2数字签名算法
- 与SM2加密基本相同
第七章 密码协议
概述
- 协议要走程序,要有多个人参与,要完成某种任务
- 对参与者完全公开、规范动作
- 有效、公平、完整
- 可实现功能
- 身份认证、密钥协商、消息鉴别、多方计算、秘密共享、零知识证明……
- 应用
- 安全通信的保密认证、电子选举、拍卖、交易
认证协议
- 目标:确认某个实体的真实性、确保信息的安全性
- 分类
- 身份认证
- 秘钥建立认证
- 消息源认证
- 消息完整性认证
- 身份证实:我想别人证实我是我;身份识别:别人是否知道是你本人
- 数据源认证:必涉及通信、涉及消息源识别、确认消息新鲜性;消息完整性:不需要这些
- 攻击
- 重放、中间人、已知密钥确定新密钥、假冒篡改替换、字典、拒绝服务……
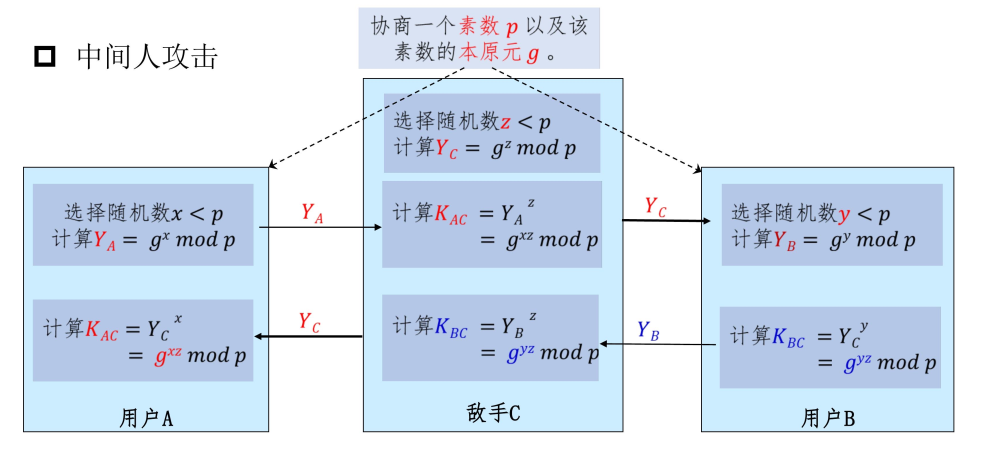
Diffie-Hellman密钥交换协议
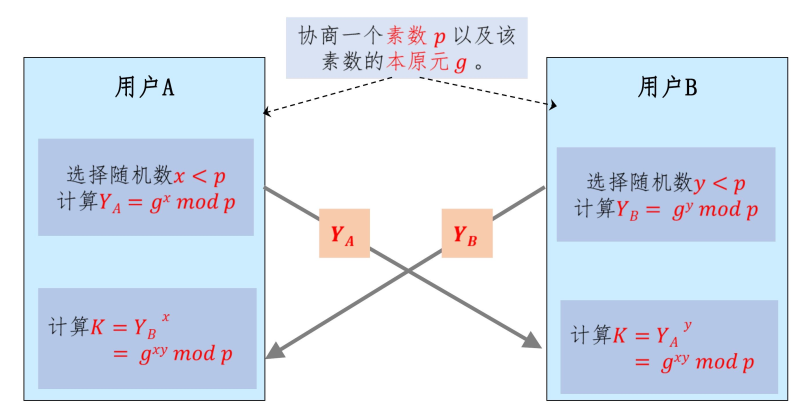
- 安全性:离散对数求解问题
- 中间人攻击

秘密共享
- 秘密s被分为n各部分成为份额或影子,由一个参与者持有:由至少k个参与者所持有的部分可以重构出s
- 此为$(k,n)$秘密分割门限方案,k为门限值
- 平面上存在唯一的k-1次多项式通过k个点,秘密为多项式$f$的$f(0)$,$f(i)$为份额

第八章 属性基加密
服务器的不可信 -> 需要用户密钥才能访问数据
基于属性的加密:密钥中含有属性信息,如医生属性的密钥可以访问病人数据
同态加密
- $E(k,F(x_1,…,x_n))=F(E(k,x_1),…,E(k,x_n))$,称加密算法E对于运算F同态
- RSA对于乘法同态
- ElGamal对于乘法同态
全同态加密
- 对于所有运算都具有同态性
- 理论上所有函数都可以由加法和乘法复合而成,于是优先考虑加法同态和乘法同态
后量子密码
- 基于Hash签名体制
- 基于纠错码的公钥密码学
- 基于格的公钥密码学
- 多变量公钥密码学








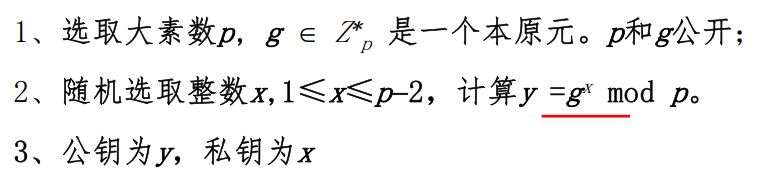

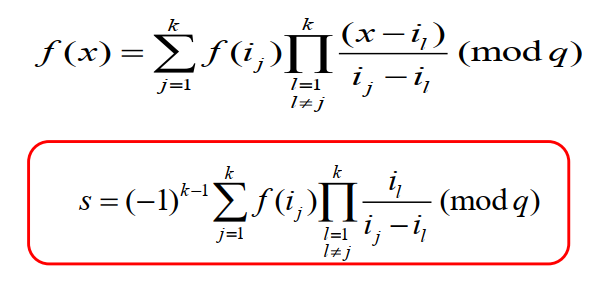

Comments 1 条评论
看不懂思密达