CSAPP Labs> Data Lab

看 CSAPP 不做 Labs，就像四大名著不看红楼梦，说明这个人文学造诣和自我修养不足，他理解不了这种内在的阳春白雪的高雅艺术，他只能看到外表的辞藻堆砌，参不透其中深奥的精神内核，他整个人的层次就卡在这里了，只能度过一个相对失败的人生。

前言

CSAPP 实际上我大一就买回来尝试开始读了，但当时看到汇编时就啃不下去了无奈弃置（现在回想起来，发现完全是当时对汇编很难懂门槛很高的刻板印象在作祟）
最近下定决心重读，花了两个多月的时间终于读得七七八八了
CSAPP 确实不负盛名，虽然有很多像虚拟内存、进程调度、并发编程这样的内容由于缺乏基础目前都还只是一知半解没能消化下来，但读过这第一遍都已经足够让我收获满满了，等以后基础更好见识更广了还要回来读第二遍乃至第三遍
久闻 CMU 给课程配套的 Labs 的大名，于是决定趁放假上手做一下

Data Lab 主要考验我们对于补码和位运算的理解，难度循序渐进，做到最后我有点寸步难行的感觉了，不得不叹服 CMU 的学生在能享受这么好的教育资源的同时也能顶住这么大的压力
不同年份的题似乎略有出入，这里做的是最新版本的
Labs 都是基于 32 位环境的，我使用的是 WSL2 的 Ubuntu 22.04 配合 32 位支持包

Lab 给了一个有多个待我们补齐的函数的源文件 bits.c、评测程序源文件 btest.c、一个 Makefile、一个非法函数检测程序 dlc 和一些杂七杂八的头文件等等
我们所需要做的就是按 bits.c 内的提示和限制补全函数以取得评测满分

Data Lab

先写个 shell 脚本方便我们多次编译和评测

make clean
make
./btest
./dlc -e bits.c

bitXor

只用按位非和按位与来实现异或运算

Legal ops：~、&
Max ops：14

运用德摩根律就能搞定，属于课程的基础知识了

int bitXor(int x, int y) {
  return ~(~(~x&y)&~(x&~y));
}

tmin

返回一个最小有符号数的补码

Legal ops：!、~、&、^、|、+、<<、>>
Max ops：4

也是基础知识，不多说

int tmin(void) {
  return 0x1<<31;
}

isTmax

若 x 是最大有符号数则返回 1，其余则返回 0

Legal ops：!、~、&、^、|、+
Max ops：10

最大的有符号数是 0111,…,1111，不难发现它有个性质是加 1 取反后会变回原数，我们就利用这个性质来构造出 0
值得注意的是 -1（1111,…,1111）也同样具备这个性质，需要规避

int isTmax(int x) {
  return !(x^~(x+1))&!!(x+1);
}

allOddBits

若补码的奇数位全为 1 则返回 1，其余则返回 0

Legal ops：!、~、&、^、|、+、<<、>>
Max ops：12

构造一个 1010,…,1010（0xaaaaaaaa）来进行判定
利用与运算剔除无关位，然后利用异或进行判定

int allOddBits(int x) {
  int eq=((0xaa<<24)|(0xaa<<16)|(0xaa<<8)|0xaa);
  return !((x&eq)^eq);
}

negate

有符号正数转有符号负数

Legal ops：!、~、&、^、|、+、<<、>>
Max ops：5

原码和补码之间的转换，也是基础知识了

int negate(int x) {
  return (~x+0x1);
}

isAsciiDigit

判断数字是否在 0x30 和 0x39 之间，是则返回 1，否则返回 0

Legal ops：!、~、&、^、|、+、<<、>>
Max ops：15

将 x>=y 转化为 x-y>=0

int isAsciiDigit(int x) {
  int eq0=!(((0x39+(~x+1))>>31)&0x1);
  int eq1=!(((x+(~0x30+1))>>31)&0x1);
  return eq0&eq1;
}

conditional

实现一个三目运算

Legal ops：!、~、&、^、|、+、<<、>>
Max ops：16

构造出全 0 或全 1，然后就可以配合与运算和或运算做出分支的效果了

int conditional(int x, int y, int z) {
  int con=~(!!x)+1;
  return (con&y)|(~con&z);
}

isLessOrEqual

若 x<=y 则返回 1，否则返回 0

Legal ops：!、~、&、^、|、+、<<、>>
Max ops：12

求出差值看符号位并加上相等的判断即可
另外还需注意的是上面的计算会溢出，所以要加上异号时的返回结果防止溢出导致错误
一开始没意识到补码的补码就是它本身，导致运算符超数了（捂脸）
括号比较多，但其实 res 后面的一长串都是判断是否异号

int isLessOrEqual(int x, int y) {
  int res=!!(((x+~y+1)>>31)|(!(x^y)));
  return (res|(((x>>31)&1)&!((y>>31)&1)))&!(!((x>>31)&1)&((y>>31)&1));
}

logicalNeg

构造出逻辑非运算

Legal ops：~、&、^、|、+、<<、>>
Max ops：12

逻辑非运算：若是 0 则返回 1，其余数字返回 0
由于 0 的补码就是它本身，而其他数字不论正负做求补码运算时符号位都会变，我们可以紧抓这一点来构造 0 和 1
值得注意的是，虽然 C 标准没有对右移运算做硬性规定，但当前大部分编译器对右移运算都采用算术右移而非逻辑右移

int logicalNeg(int x) {
  return (((~x+1)|x)>>31)+1;
}

howManyBits

给定一个有符号数，返回表示这个数的补码所需的最少位数

Examples：
- howManyBits(12) = 5
- howManyBits(298) = 10
- howManyBits(-5) = 4
- howManyBits(0) = 1
- howManyBits(-1) = 1
- howManyBits(0x80000000) = 32
Legal ops：!、~、&、^、|、+、<<、>>
Max ops：90

题意也不太好理解，研究了一下 Examples 总结出的大致题意是：正数则找最高位的 1 的位数，负数则找最高位的 0 的位数，最后还要算上符号位

感觉是这个 Lab 里最难的题了，研究了好久都没有思路，无奈只能看网上的题解QAQ
思路很巧妙，但其实也很自然，采用分治的思想，对最高位做二分搜索
更巧妙的是这个方法可以只用一个中间变量完成一段位数的 0 的判定、移位数目的分支和计数
中间变量比较多，需要注意题目规定的代码规范
还看到有用掩码进行计算的，这里就不介绍了

int howManyBits(int x) {
  int b16,b8,b4,b2,b1;
  int sign=x>>31;
  x=(sign&~x)|(~sign&x);
  b16=!!(x>>16)<<4;
  x=x>>b16;
  b8=!!(x>>8)<<3;
  x=x>>b8;
  b4=!!(x>>4)<<2;
  x=x>>b4;
  b2=!!(x>>2)<<1;
  x=x>>b2;
  b1=!!(x>>1);
  x=x>>b1;  
  return b16+b8+b4+b2+b1+x+1;
}

floatScale2

将一个单精度浮点数以无符号数的形式传入，要求我们以无符号数的形式返回这个浮点数 *2

Legal ops：Any integer/unsigned operations incl. ||、&&，also if、while
Max ops：30

之前看 CSAPP 的时候没怎么认真看浮点数那块的内容，跑回去补了一下

我们需要根据 IEEE 浮点标准对浮点数的各个字段进行处理来达到 *2 的目的
首先需要拆分符号位 s、阶码 exp和小数字段 frac
然后先判定非规格化数，非规格化数 *2 就相当于小数字段整体左移 1 位
然后再来判断规格化数，规格化数 *2 就相当于将阶码 +1，如果 *2 后超出规格数的表示范围，那么就将它转变成无穷
对于无穷和 NaN 我们直接返回它本身即可

unsigned floatScale2(unsigned uf) {
  unsigned s = uf & 0x80000000;
  unsigned exp = uf & 0x7f800000;
  unsigned frac = uf & 0x007fffff;
  if(!exp) frac=frac<<1;
  else if(exp^0x7f800000){
    exp=exp+0x00800000;
    if(!(exp^0x7f800000)) frac=0;
  }
  return s|exp|frac;
}

floatFloat2Int

将一个以无符号整数表示的单精度浮点数转化为整数，如果为特殊值则返回 0x80000000

Legal ops：Any integer/unsigned operations incl. ||、&&，also if、while
Max ops：30

对于非规格化数则返回 0
对于特殊值则返回 0x80000000
对于规格化数则根据阶码 E=exp-127 对小数进行移位即可
最后用符号位判定正负值

int floatFloat2Int(unsigned uf) {
  int s,frac,E,res;
  s=uf>>31;
	frac=(uf&0x007fffff)|0x00800000;;
	E=((uf>>23)&0xff)-127;
  if(E<0) res=0;
  else if(E>31) res=0x1<<31;
  else if(E>23) res=frac<<(E-23);
  else res=frac>>(23-E);
  return s?(~res+1):res;
}

floatPower2

求$2.0^x$，若结果太小则返回 0，若太大则返回正无穷

Legal ops：Any integer/unsigned operations incl. ||、&&，also if、while
Max ops：30

单精度浮点数的指数范围为 [-126~127]，界外的值需要隔离出来
根据阶码和指数的关系，我们可以直接将合法的值转化为阶码字段得到结果

unsigned floatPower2(int x) {
  int res;
  if(x<-126) res=0;
  else if(x>127) res=0x7f800000;
  else res=(x+127)<<23;
  return res;
}

后记

至此，我们完美完成了 Data Lab

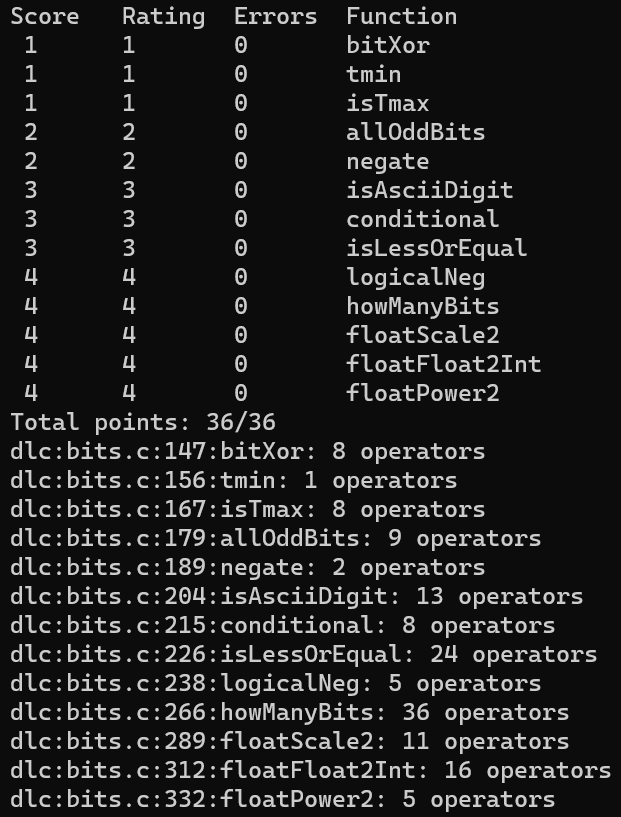
书里这一章和这个 Lab 初看感觉没什么，但实际上整个过程挺烧脑折磨的，整整耗费了我两晚有多才做完，不过最终还是挺有收获和成就感的
现在对于机器里信息的表示、运算和转换有了一个更清晰的认知，做 Lab 前并没有意识到自己在这章有这么多没理解透彻的内容（虽然现在对浮点数的表示还是有点迷糊），挺庆幸动手完成了这个 Lab

下一个就是大名鼎鼎的 Bomb Lab 了，看了一下感觉跟 CTF 里的 RE 题还挺像，后面的 Attack Lab 和 Buffer Lab 也涉及到了 ROP，有点期待起来了

お帰りなさい~